02 逻辑与沟通,怎样才能讲出有逻辑的话?
02 逻辑与沟通,怎样才能讲出有逻辑的话?
你好,欢迎来到第 02 课时—— “与”“或”“非”:怎样才能讲出有逻辑的话?
我们都知道,语言沟通的背后是说话人逻辑思维的过程,单句与单句间、事件与事件间,都是靠关联词联系起来的,所以这节课我将从数学逻辑的角度,向你论述语言沟通背后的原理。
我将先向你介绍这一课时的根本思维原则 —— MECE 原则,再从“与”“或”“非”“异或”,以及“文氏图”这些运算方式出发,带你深入剖析沟通表达中的关联词。
从日常沟通看逻辑
在日常的沟通中,代表逻辑关系的词汇有很多,例如“而且”“或者”“但是”“如果…那么…”“因为…所以…”等关联词。
在我们使用这些词汇的时候,其实都是在表达事件之间的逻辑关系,如果你的逻辑是混乱的或者是不清晰的,就会出现关联词乱用的情况,从而造成沟通效率低下,甚至传递错误信息。
我们先来看一个例子,事情背景是某个系统需要从 A 环境迁移过渡至 B 环境,大家可以注意一下这段话有什么表达不妥之处。
“为了保证系统的稳定过渡, 并且 保证在过渡期,各个使用方的需求正常迭代, 因此
系统拟定共分为三期:过渡期、实验期、切换期。其中,过渡期采用某技术,保证数据系统打通;实验期通过 AB 实验,验证流程正确。”
从字面来看,我们能脑补出说话者要做什么事情,以及做这些事情的目的和方法。但是,从逻辑的视角来看,上面一段话至少包含了以下几个问题:
- “保证系统的稳定过渡”和“在过渡期内,各个使用方的需求正常迭代”,这二者的语意是包含关系,并不是并列关系,用 “并且” 进行连接,不合理。
- 为了保证系统的稳定过渡,因此需要分为三期。这里构不成因果关系,用 “因此” 进行连接,不合理。
- 过渡期怎样怎样,实验期怎样怎样,切换期呢?丢了一个重要环节,不知道需要做什么事情。
这些问题看似是语文问题,实际是背后思考的逻辑问题。
而逻辑思维对于程序员的代码编程能力非常重要,所以接下来我将向你介绍“MECE 原则”,帮你提升逻辑能力,MECE 原则非常重要,它将贯穿整个课时内容。
MECE 原则,提升逻辑思维水平
MECE 原则(Mutually Exclusive Collectively
Exhaustive)的中文意思是“相互独立,完全穷尽”,简而言之,能够做到不重叠、不遗漏,兼顾排他性和完整性。
MECE 原则是麦肯锡提出的一种结构化思考方式,无论是报告撰写,提案演讲,业务分析,它是一种很好的思维方式。
它就像是切比萨一样,一个大比萨,用 4 刀切成了 8 份,每一份之间彼此不重叠(排他);所有的小比萨不遗漏(完整)地合在一起,又还原了大比萨。

我们来看个例子,公园的票价问题。公园的门票价格是 20 元,优惠票包括了老人票和儿童票。价格制度为:
- 不到 10 岁的儿童免费;
- 10 岁以上的未成年人半价;
- 60 岁及以上的老人免费;
- 其他成年人无折扣。
我们用 MECE 原则来看一下这里的定价制度,就会发现这个制度不满足“不遗漏”“不重叠”的要求。比如,这让 10 岁的小琳很尴尬,她到底是算不到 10
岁免费呢?还是 10 岁以上未成年的半价呢?至少,从上面的描述是看不出来的。
用程序语言来看,上面价格对应的代码就是:
org_price = 20
age = 10
if age < 10:
discount = 0.0
if age > 10 and age < 18:
discount = 0.5
if age > 60:
discount = 0.0
if age >= 18 and age < 60:
discount = 1.0
final_price = discount * price
显然,当 age 为 10 的时候,程序不会走任何一个策略分支,于是代码会出现错误。
在解决类似的逻辑问题时, 一定要注意所有边界值的可能性 。原则上,每个可行值(尤其是边界值)能且只能落在一个策略分支中。
一个常用的分析方法就是画线法,如下图所示。画一根数轴,代表所有的可行值,再使用 if 语句分解问题,空心点表示开区间,实心点表示闭区间。
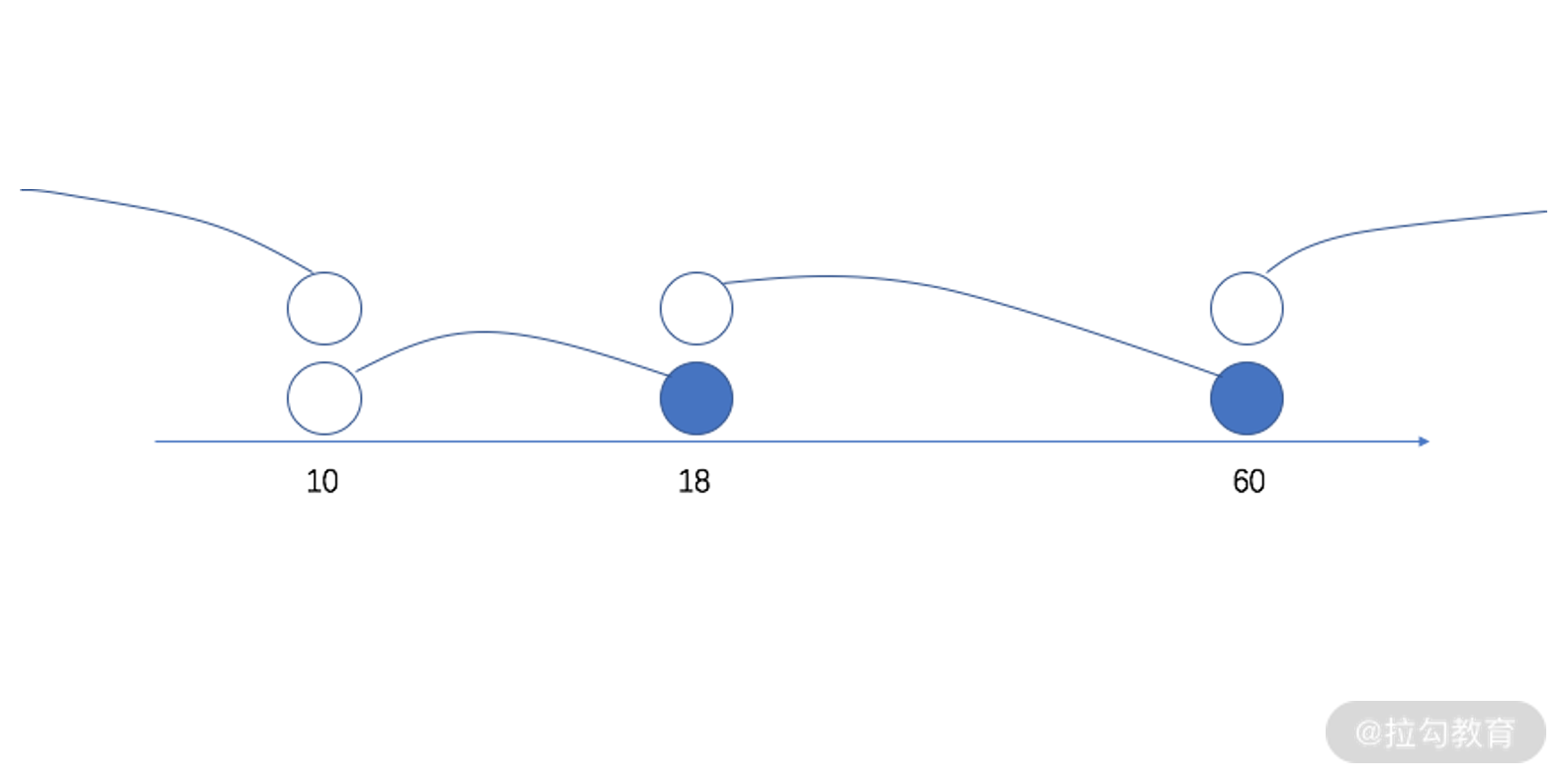
画线法
逻辑运算:“与”“或”“非”“异或”
接着我们来深入到逻辑的运算,首先看一下命题的概念。
命题是一个描述客观事物的陈述,它包含了正确或错误两个可能性。
- 如果命题正确,我们一般用 true 或 1 来表示;
- 如果命题错误,我们一般用 false 或 0 来表示。
有了命题,我们就可以对命题和命题进行逻辑计算。这很像有了数字之后,就有了加减法。逻辑运算的对象是命题,它根据命题的真假进行计算,并且最终再输出真或者假,作为结果。
逻辑的运算,通常有“与”“或”“非”,以及叠加在这之上的“异或”。
1.最基础的“与”“或”“非”。
- 逻辑 “与” —— A 并且 B,在 Python 语言中也记作 A and B。只有命题 A 和命题 B 同时为真的时候,A and B才是真,否则都是假;
- 逻辑 “或” —— A 或者 B,在 Python 语言中也记作 A or B。命题 A 或者命题 B 有一个为真的时候,A or B 就是真,否则为假;
- 逻辑 “非” ——不是 A,在 Python 语言中也记作 notA。命题 A 为假的时候,not A 就是真,否则为假。
值得一提的是,在不同学科、不同编程语言中,对于逻辑的“与”“或”“非”的符号表示并不相同,可能的符号有:
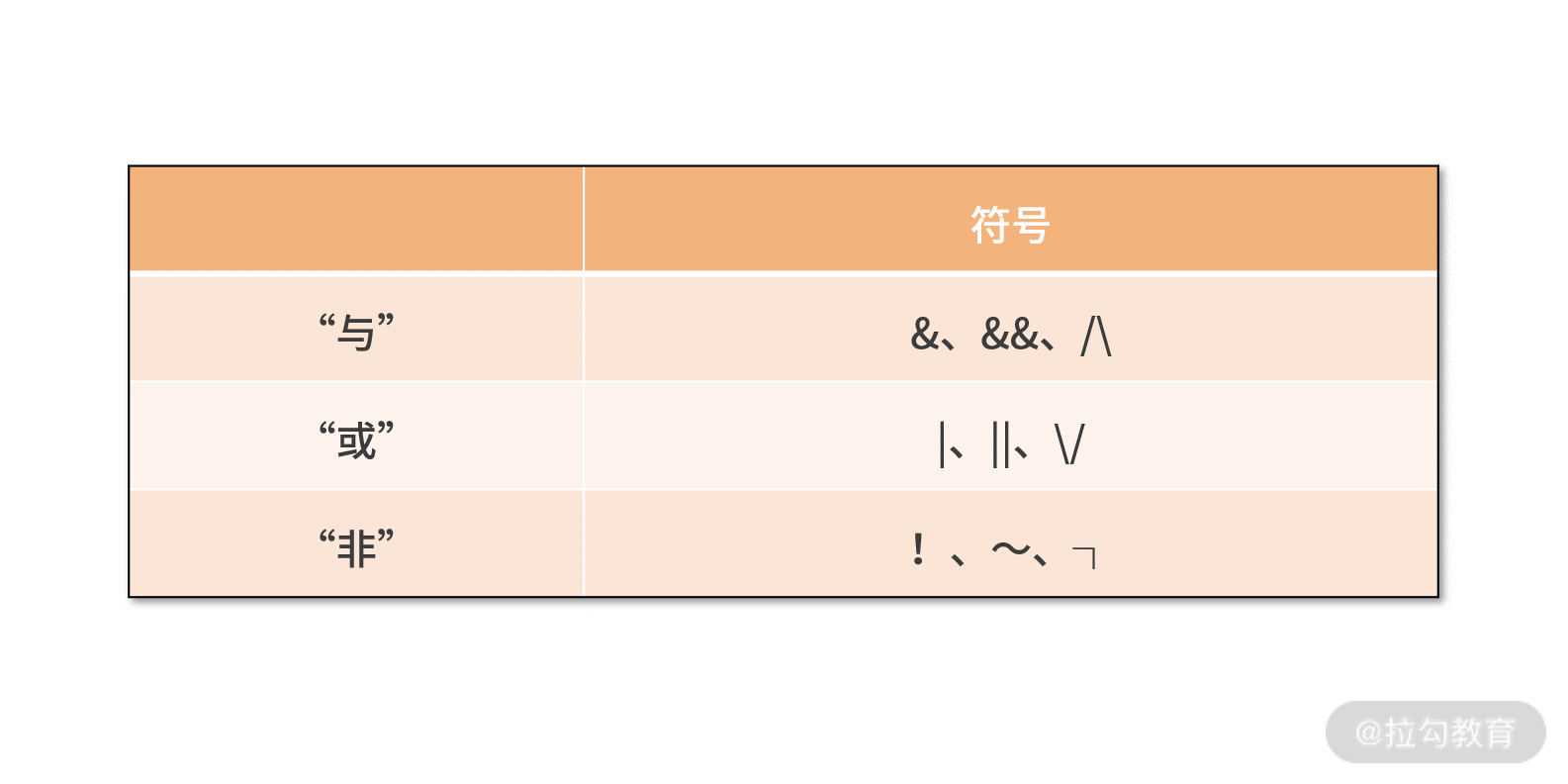
虽然符号不一样,但是计算结果都是一样的。
2.从文氏图看“异或”
“异或”在 Python 语言中也记作A^B 。命题 A 和命题 B 的真假不同时,则 A^B 为真,否则为假。一个好的记忆方式是,异为 1,即 A
和 B 的真假性相异(不同),则结果为 1(为真)。
一个形象判断逻辑关系的方法是,便是 文氏图 ,如下图所示,假设在文氏图中有两个命题 A 和
B,用椭圆形的区域表示一个命题为真的地方,而椭圆区域外则表示这个命题为假的区域。
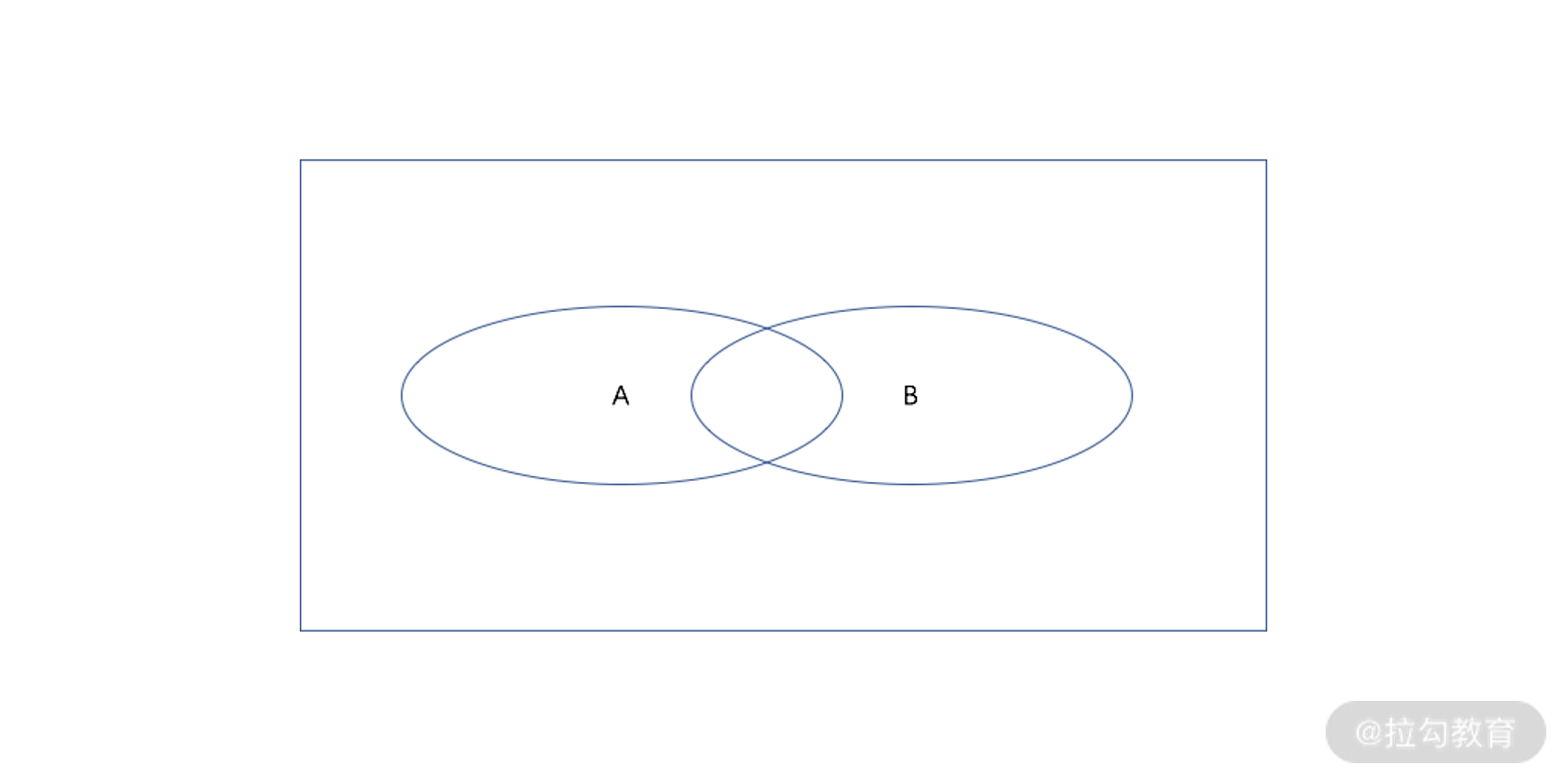
文氏图
通过分析两个命题的椭圆形,在图中的位置关系,就能得到每个运算的结果。接下来,我先用文氏图演示“与”“或”“非”的运算过程,最后再向你讲解什么是“异或”。
- “与” A and B
根据逻辑运算的定义,如下图所示,A and B 为真的区域就是,椭圆 A 和椭圆 B的交集(蓝色区域)。
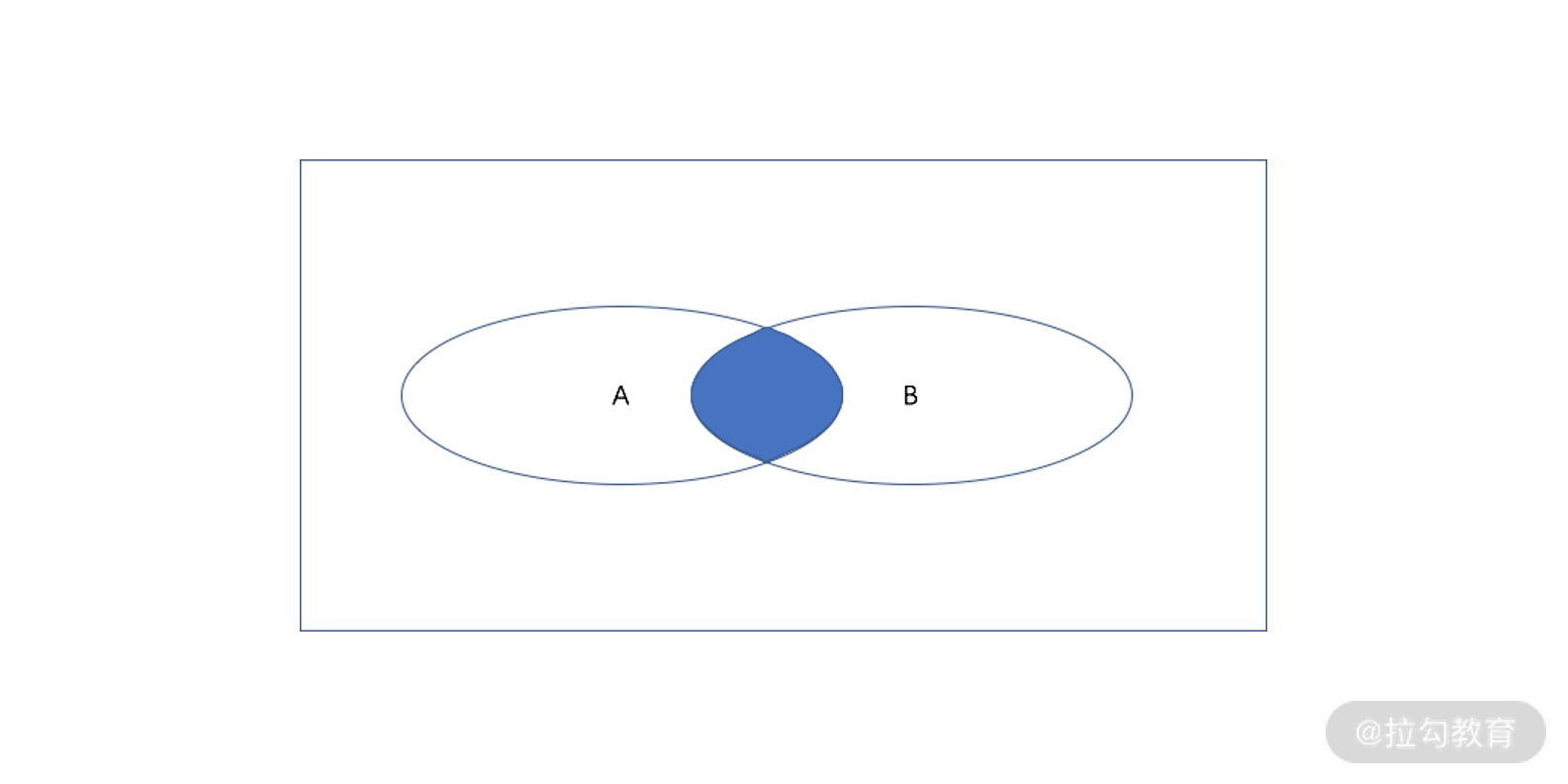
A and B 文氏图
- “或” A or B
如下图所示,A or B 为真的区域,便是椭圆 A 和椭圆 B 的并集(蓝色区域)。
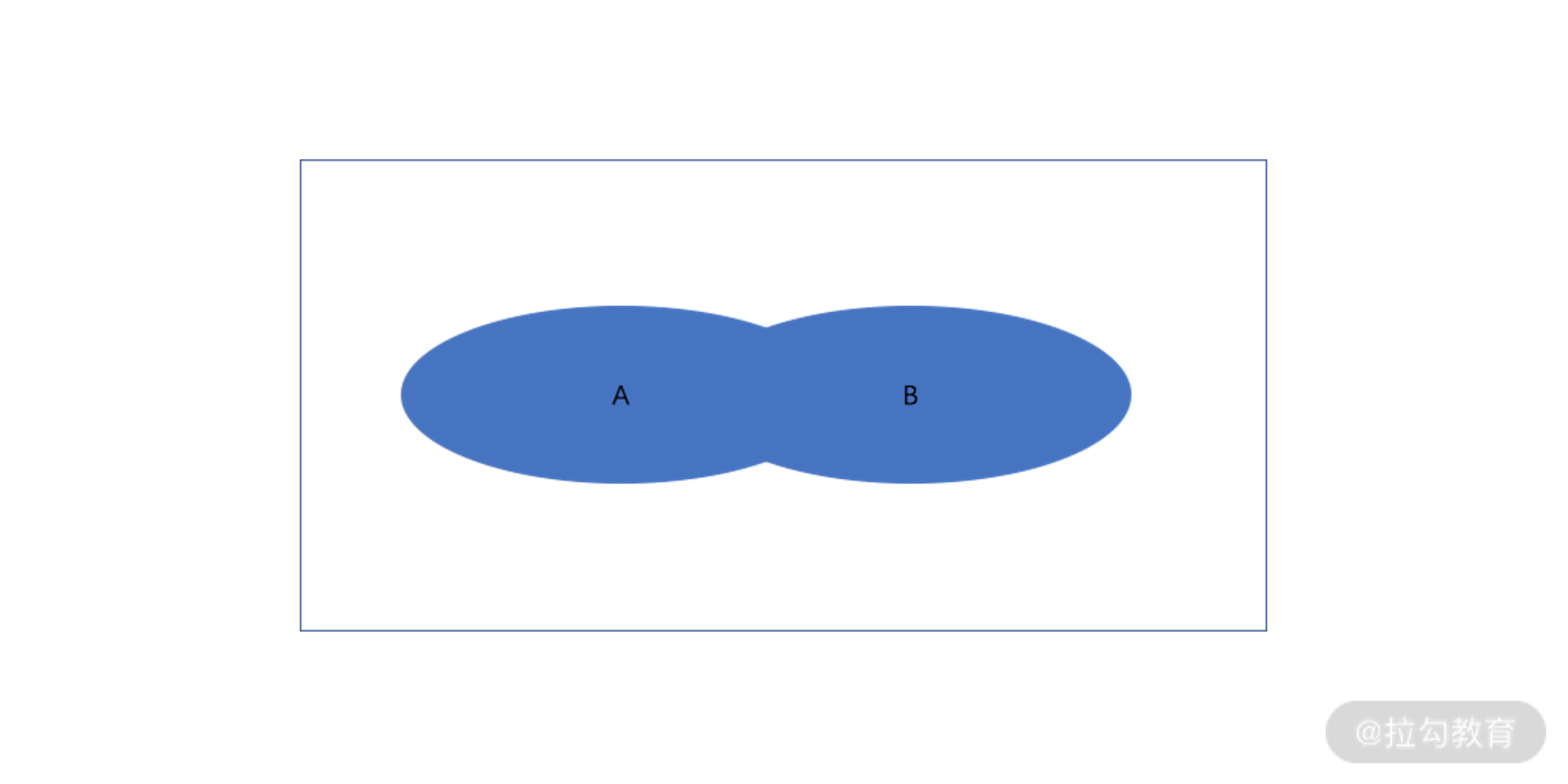
A or B 文氏图
- “非” not A
如下图所示,not A 为真的区域,便是椭圆 A 以外的部分(蓝色区域):
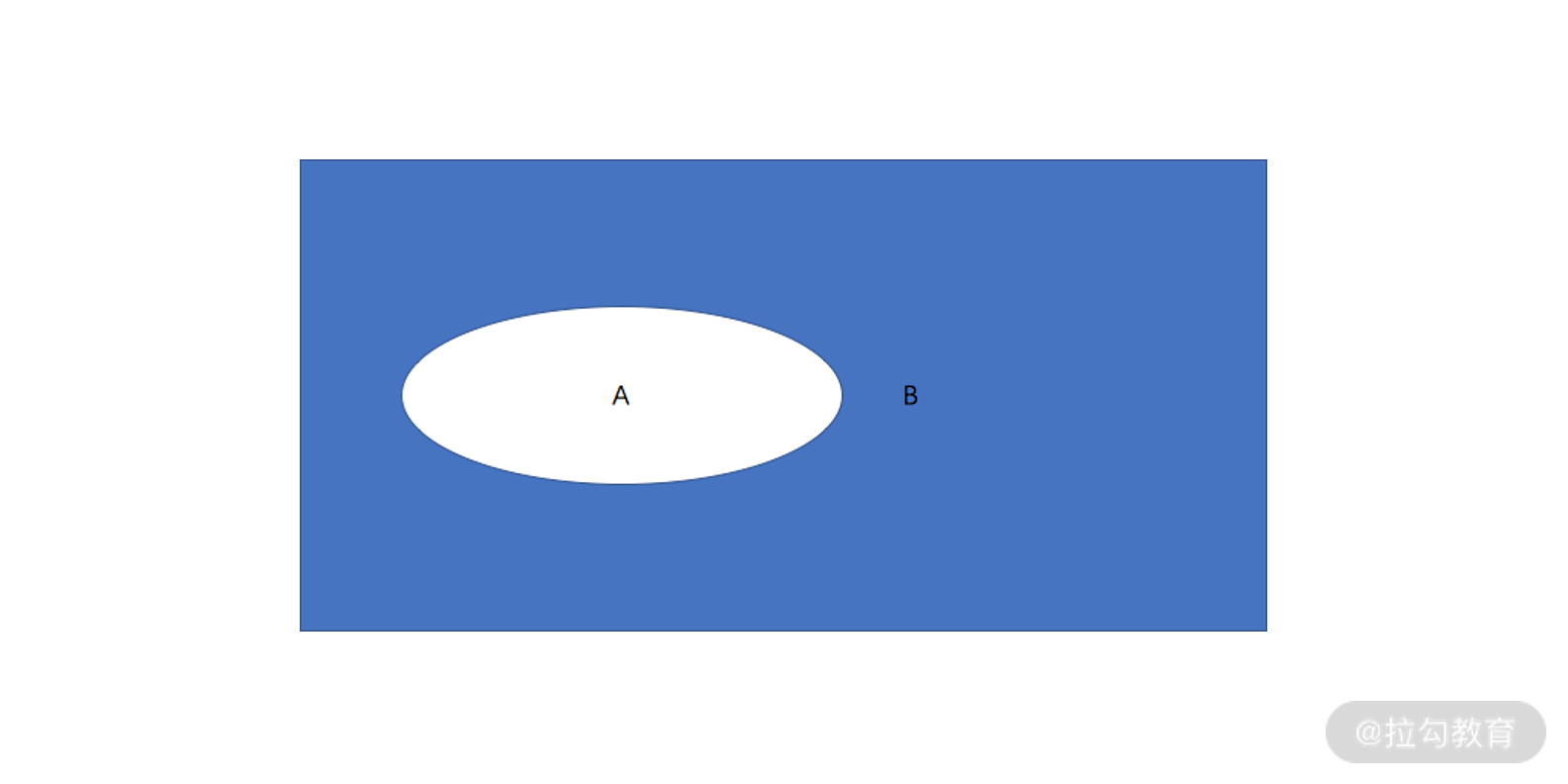
not A 文氏图
- “异或” A^B
A^B,表示 命题 A 和命题 B 的真假不同,也就是真假相异,故是下方文氏图的蓝色区域。
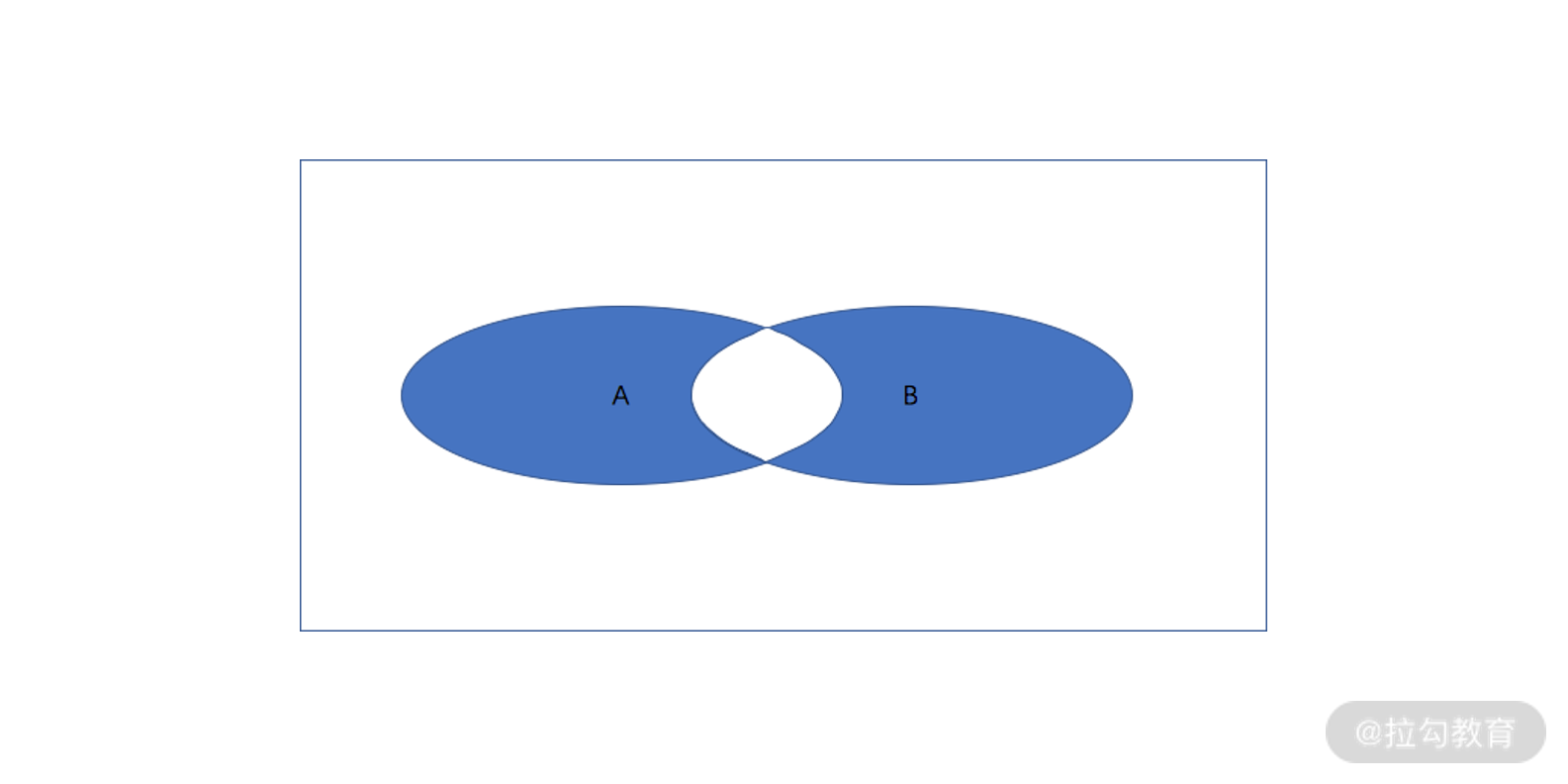
A^B 文氏图
你会发现, “A^B”的蓝色区域,就是上面“A or B”区域减去“A and B”区域,即A^B = (A or B) - (A and B) 。
讲完命题的逻辑运算后,我们进入工作实践场景,向你讲解工作中的命题逻辑处理问题。
逻辑处理:MECE 原则与代码
在工作中需要处理命题的逻辑关系时,一定要在满足上文提及的 MECE 原则 的基础上进行代码开发。
1.不遗漏原则
当你在处理逻辑关系时,不管有多少个可能的 if 语句,哪怕你觉得你已经在 if 中穷举了所有的可能性,也尽可能用 else 进行一个兜底,
这是对代码潜在风险的规避 。
例如,下面一段代码从结构来看,它虽然没有错误,但不利于解读、维护。
def fun(x):
if x == 1: #命题A
return 1
if x == 2: #命题B
return 2
不管命题 A 和命题 B 是否包含了全部的可能性,你都需要用个 else 进行兜底,因此更好的方式是:
def fun(x):
if x == 1: #命题A
return 1
if x == 2: #命题B
return 2
else: #兜底
return 0
2.不重复原则
就说明 每个可能的输入,只能进入唯一 一个策略分支 ,否则就有可能造成结果不受控制。这就说明,在代码开发中,尽可能少用多个 if 语句,而改用
elif 语句。
elif 是 else if 的合体,功能上他们二者完全可以互相替代,从逻辑的表达来看,elif 更像是对 if 的兜底。
例如下面一段代码,风格就有些不好,容易引起不必要的代码风险。
def fun(x,y):
a = 0
if x < y: #命题A
a = 1
if x >= y: #命题B
a = 2
else: #兜底
a = 0
return a
不管你的命题 A 和命题 B 是否有交集,你都需要尽可能少地使用多个并列无关的 if 语句,而改用 elif,例如:
def fun(x,y):
a = 0
if x < y: #命题A
a = 1
elif x >= y: #命题B
a = 2
else: #兜底
a = 0
return a
从数学思维和代码角度,深入了解“逻辑”后,我们重新回到日常沟通中。
从逻辑回归到沟通
我们最开始提到了很多日常沟通的词语,例如 “而且” “或者” “但是” “如果…那么…” “因为…所以…”等关联词。
那么,这些关联词跟我们这个课时讲到的 “与” “或” “非” 有什么关系呢?我们结合逻辑运算和文氏图进行分析。
1.“而且”与“或者”
“而且”,顾名思义,就是 A and B。例如,小琳很漂亮(A),同时小琳很聪明(B)。经过逻辑运算后,得到小琳漂亮且聪明(A and B)。
“或者”,顾名思义,就是 A or B。例如,这个暑期,小琳打算去海南,否则小琳就打算去辽宁。经过逻辑运算后,得到这个暑假,小琳打算去海南或者辽宁(A or
B)。
你可以发现“漂亮”和“聪明”,“海南”和“辽宁”都是相互独立的。所以你在使用“而且”和“或者”沟通时,要注意命题 A 和命题 B 也最好是相互独立的,
也就是 A 与 B 应符合上文讲的 MECE 中的不重复原则。
下面我将通过三个反例说明问题:
- 例1,小琳很聪明漂亮(A), 而且 小琳很聪明(B)。
虽然语义上无误,读者也能理解,但从沟通的角度来看,这句话非常不妥帖。
- 例2,为了保证系统的稳定过渡(A),并且(即而且)保证在过渡期内,各个使用方的需求正常迭代(B)。
此时,命题 A 显然包括了命题 B,与例1 如出一辙。
- 例3,小琳是东北人(A), 或者 小琳是北方人(B)。
“北方”包含了“东北”,相互重复,在表达上绕了一个大弯,仅表达小琳是北方人。
通过这三个反例我们可看出,缺乏逻辑性的关联词,虽然不会影响语义表达的正误,但却会让沟通变得冗杂,不够直接明了,从而降低了沟通效率。
所以,沟通表达与逻辑思维有着直接关系。接下来,我将讲解“因为…所以…”和“虽然…但是…”这对更体现逻辑思维的关联词,也请你好好揣摩一下这对关联词之间的相互逻辑关系。
2.因为……所以……
“因为…所以…”,是一种逻辑推理,即由 A 推导出 B。
“因为…所以…”的文氏图表达如下图所示,A 包含于 B,B 包含了 A,在 A 区域内,也一定会在 B 区域内,因为存在于 A,所以存在于
B,这是个 由“小”推导出“大” 的过程。
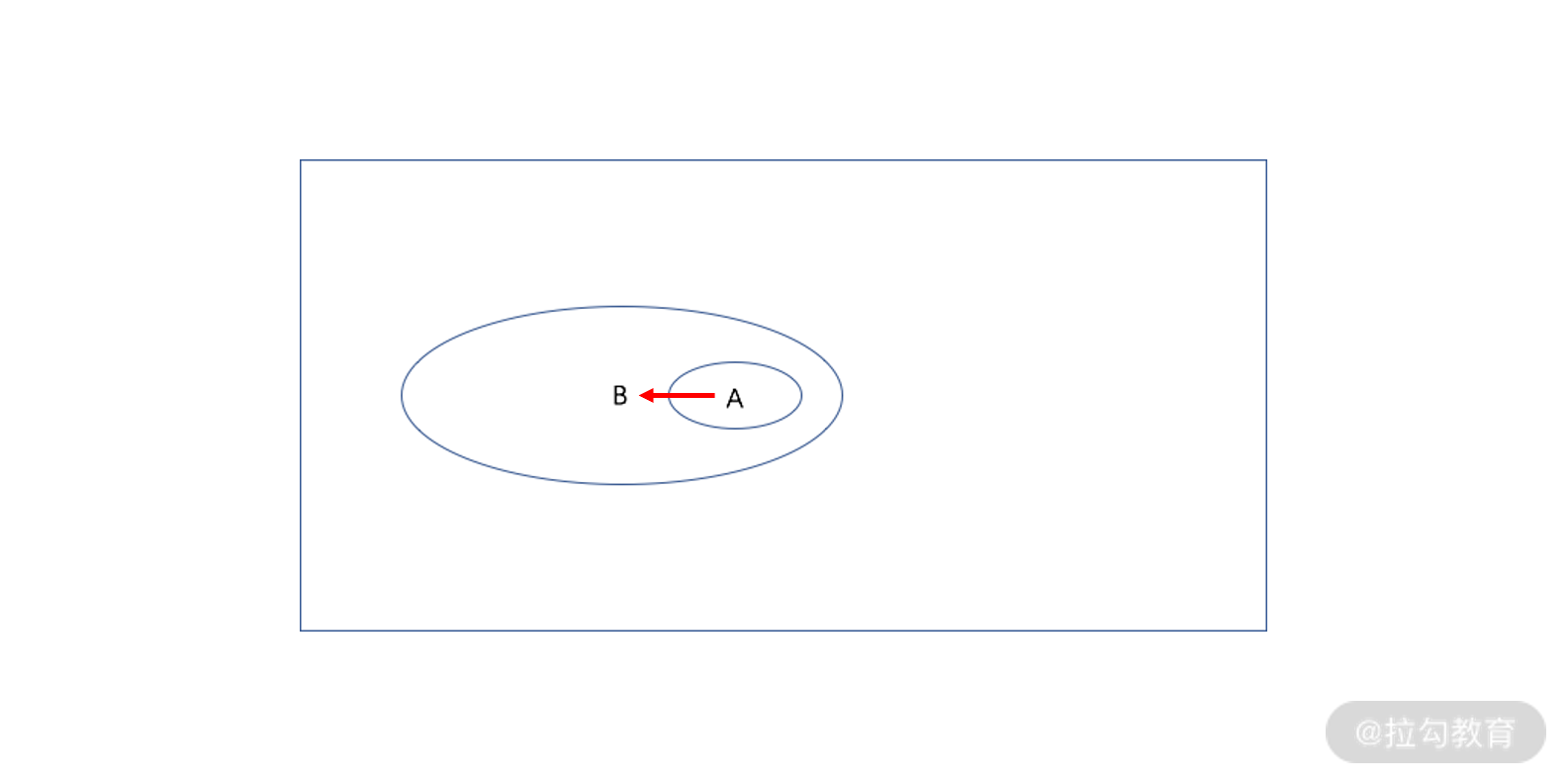
“因为…所以…”文氏图
在使用“因为…所以…”沟通时,一定要注意命题之间是否具备了 充足的因果关系 。否则,就会出现让人反感的逻辑错误。
先举一个恰当的例子:
因为小琳聪明漂亮(命题 A),所以小琳很漂亮(命题 B)。
可以看出命题 A 和 命题 B 两者有充足的包含和被包含的因果关系。
下面再举一个反例:
因为 要保证系统的稳定过渡,并且保证在过渡期内,各个使用方的需求正常迭代,所以系统拟定共分为三期:过渡期、实验期、切换期。
长话短说,即“因为要保证稳定过渡,所以拆分为三期”。
那么要保证稳定过渡,就必须拆分为三期吗?显然并不是,拆分为四期、五期,全凭开发者自己的设计方案,都是可以的,显然这两者不具备强烈的因果关系。
3.虽然……但是……
再来看看“但是”,一般也用作“虽然…但是…”,它表示的是一种转折关系,比如:
虽然小琳学习成绩不好,但她一直很努力。
在人们的潜意识中,成绩好的人一定是努力的人,这就是“ 因为 她成绩好(A), 所以
她是个努力的人(B)”的默认关系;反之,努力的人(B),学习成绩不一定很好(非 A),这就构成了转折,于是得到“ 虽然 小琳成绩不好(非 A),
但是 她很努力(B)”。
在这一例子的逻辑过程中,你会发现 “虽然(非A)…但是(B)…” 这个关联词与 “因为(A)…所以(B)…” 刚好相反。
正如下图所示,“因为A,所以B”,也可以用作描述“虽然非A,但是B”。
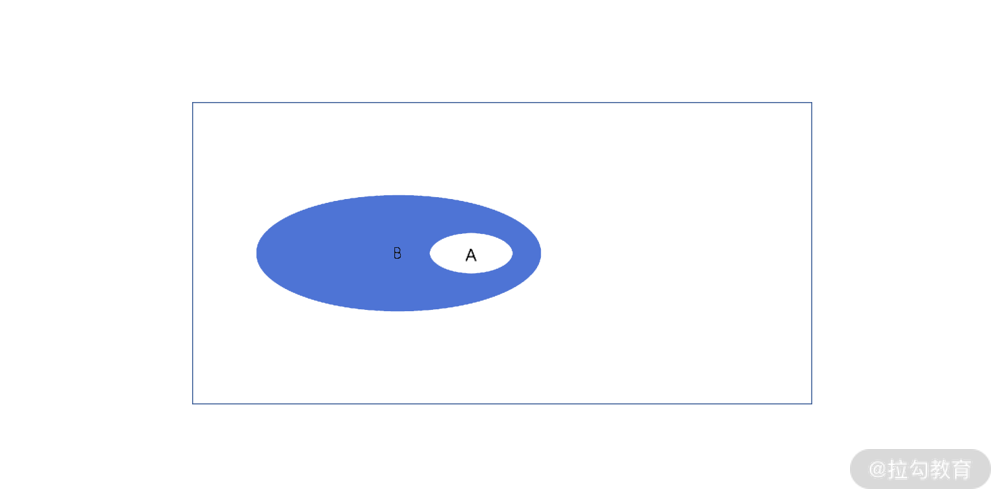
“虽然…但是…”文氏图
所以我们在验证“虽然…但是…”这个关联词是否使用妥帖时,可以先将其转为因果关系,我会通过以下几个例子向你演示这一过程。
- 虽然小琳不是单身(非A),但是她是个东北人(B)。
将这句话转为因果关系,则有“因为小琳是单身(A),所以她是东北人(B)”。显然,这里就构不成任何的因果关系了。(✖️)
- 虽然小琳成绩不太好(非A),但是她并没有自暴自弃(B)。
将这句话转为因果关系,则有“因为小琳成绩好(A),所以她没有自暴自弃(B)”。显然,这里的因果性很强。这里的“但是”使用得非常恰当。(☑️)
- 虽然小琳不是单身(非A),但是她的成绩依旧很好(B)。
将这句话转为因果关系,则有“因为小琳是单身(A),所以她的成绩好(B)”。这里的因果性就很弱了,也因此“但是”使用得并不完全恰当。(✖️)
在日常生活中,很多时候的“但是”是被误用的,虽然日常沟通中,不必过度关注这些瑕疵,但在书面语的环境下,就会不太妥帖。
小结
“怎样才能讲出有逻辑的话?”学完这一课时的你,对这个问题肯定有了自己的答案,并对“逻辑”与“沟通”之间的关系有了更深的理解。
其实,在日常沟通中的很多场景下,逻辑词的使用并没有那么高的要求,人们往往会根据自己的用词偏好去说话,也不必过度吹毛求疵。
但是,当你掌握了很好的逻辑思维方式后,你与人沟通表达时,便会更有说服力,沟通效率也会大大提升;分析事物问题时,也会更加周密完善,一针见血。
比如,当你站在逻辑的视角来重看上文的这些例子时,你就会发现很多逻辑并不规范,尤其是使用了文氏图这一工具之后,你便能一针见血地看到本质,清晰地分析出这些逻辑关系背后的漏洞。