09 似然估计:如何利用 MLE 对参数进行估计?
09 似然估计:如何利用 MLE 对参数进行估计?
你好,欢迎来到第 09 课时——似然估计:如何利用 MLE 对参数进行估计?
前面我们学会了如何计算概率,这一讲我们学习如何利用概率对某个参数进行估计。在读书的时候,你一定接触过极大似然估计,它是数学课程的难点之一,它名字背后的含义,以及它的推导过程都非常复杂,需要你对它有深刻的理解。
不过,有了前面“形式化定义”“概率计算的加乘法则”和求函数最值的“求导法”“梯度下降法”的知识储备,相信极大似然估计也能迎刃而解。
白话理解“极大似然估计”
如果你是刚刚学习概率,极大似然估计这六个字一定会让你产生不解。
似然
(Likelihood),可以理解为可能性,也就是概率。举个例子,某个同学毕业于华中科技大学这样的工科院校,那么这位同学是男生的可能性(或者说概率、似然)就更大;相反,某个同学毕业于北京外国语学院这样的文科院校,那么这位同学是女生的可能性(或者说概率、似然)就更大。
那么反过来思考,如果大漂亮是个美丽又可爱的女生,现在有两个候选项:A.大漂亮毕业于华中科技大学;B.大漂亮毕业于北京外国语学院。在对其他信息都毫不知情的情况下,你更愿意相信哪个呢?很显然,相信
B 是更好的选项,因为 B 的概率(或者说似然)更大。
其实,在刚刚的思考逻辑中,我们已经不知不觉地用了极大似然估计的思想了—— 估计 (Estimate),用大白话说就是“猜”。
例如,你对于大漂亮毕业院校的“估计”是她来自北京外国语学院;这就是说,你“猜测”大漂亮毕业于北京外国语学院。那么,为何你猜测她毕业于北京外国语学院,而不是华中科技大学呢?原因就是前者的可能性更大,而后者可能性更小。换句话说,从可能性的视角看,前者是个
极大 值(Maximum)。
我们将上面思考过程的 3 个关键词“ 极大 (Maximum)”“ 似然 (Likelihood)”“ 估计
(Estimate)”给提炼出来,就得到了极大似然估计这个方法,通常也可以用这 3 个单词的首个字母来表示——MLE。
极大似然估计的方法路径
从刚才的例子不难看出,极大似然估计做的事情,就是
通过已知条件对某个未知参数进行估计,它根据观测的样本构建似然函数,再通过让这个函数取得极大值,来完成估计 。接着,我们用数学语言来描述整个过程。
极大似然估计的流程可以分为 3 步,分别是似然、极大和估计。
- 第一步 似然 ,即根据观测的样本建立似然函数,也是概率函数或可能性函数。 这个步骤的数学表达如下:假设观测的样本或集合为 D,待估计的参数为 θ。则观察到样本集合的概率,就是在参数 θ 条件下,D 发生的条件概率 P(D|θ)。这就是似然函数,也是极大似然估计中最难的一步。
- 第二步 极大 ,也就是求解似然函数的极大值。 你可以通过求导法、梯度下降法等方式求解。这个步骤的数学表达就简单许多,即 max P(D|θ)。
- 第三步 估计 ,利用求解出的极大值,对未知参数进行估计。

利用这 3 步就完成了极大似然估计的整个流程。
接下来,我们将这个方法路径用在对“大漂亮毕业院校的极大似然估计表达”上。
- 第一步 似然
我们观测的样本结果 D 是“大漂亮是个女生”,待估计的变量 θ 是“大漂亮毕业于哪个学校”。这样,似然函数就是 P(D|θ) =
P(大漂亮是个女生|大漂亮毕业于 θ 学校),其中 θ∈(北京外国语学院,华中科技大学)。
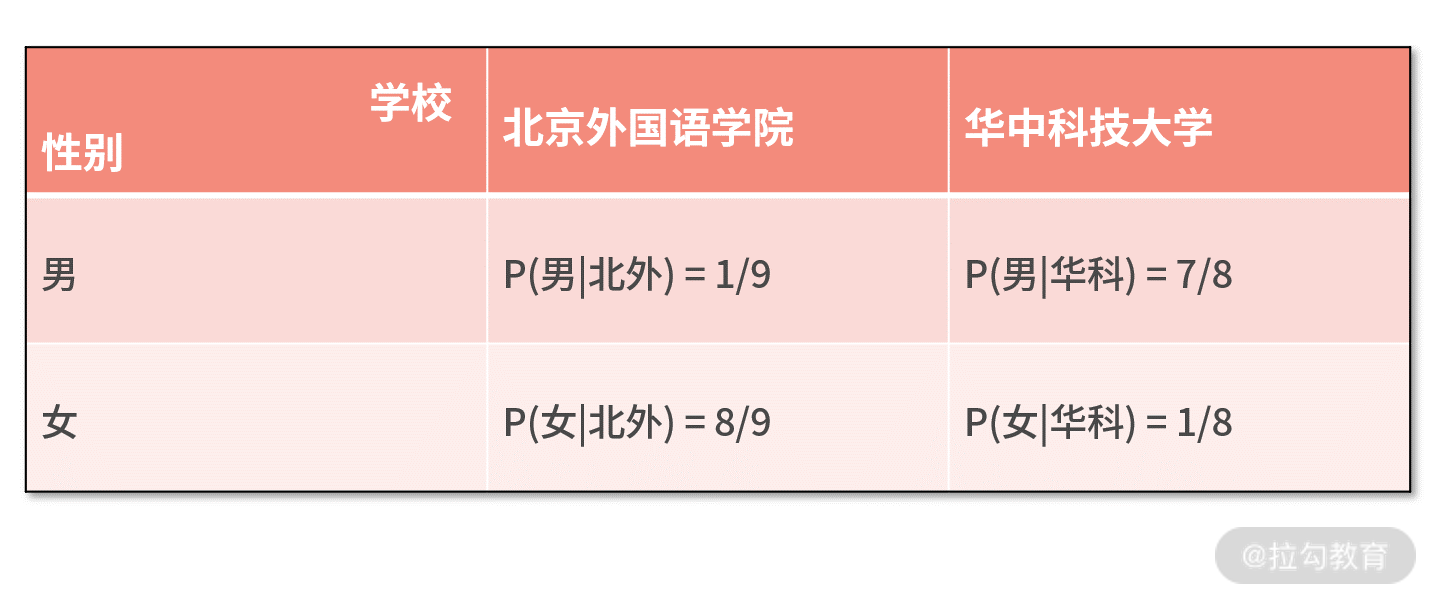
接着,我们还需要了解工科院校、文科院校的男女比例情况,把似然函数写出具体的数字表达。假设华中科技大学的男女比例为 7:1,北京外国语学院的男女比例为
1:8,则有下表的概率值:
- 第二步 极大
有了前面的信息,我们就能求解似然函数的极大值了。似然函数中参数 θ
是离散值,只有两个可能的取值。因此,我们既不需要求导法,也不需要梯度下降法,只需要把两种可能性都算一下,再进行比较就可以了。
不难发现,因为 P(女|北外)=8/9 > P(女|华科) = 1/8,所以似然函数的极大值是 8/9。
- 第三步 估计
求解出似然函数的极大值之后,我们利用取得极大值的参数值作为结果,则有
极大似然估计的拓展
前面的例子很简单,而实际中你可能还会遇到很复杂的拓展问题。
1.第一个复杂的拓展问题,为单样本拓展为多样本
刚刚的观察样本集合中,只有一个样本(即大漂亮是个女生)。而如果有多个样本又该怎么办呢?
此时我们需要用到概率计算的乘法法则。通常,我们都会认为同一个事件的不同观测结果是独立的,因此可以用乘法法则计算它们共同发生的概率。
这个过程用数学语言表达,就是假设观测的样本集合为 D = (d1,d2,d3……dn),待估计的参数为θ,则似然函数 P(D|θ) =
P(d1,d2,d3……dn|θ)。
因为观测样本独立,满足 P(AB) = P(A)·P(B),则有

2.第二个拓展问题,是似然函数到对数似然函数
刚刚的推导结果非常吓人。大型连乘算式中,直接求解最值是非常困难的。不过,庆幸的是数学中有个化乘法为加法的函数——对数函数。因为对数函数是单调的,所以在化乘法为加法的过程中,不会改变最大值发生的位置,即
ln(xy) = ln x + ln y。

MLE 梳理
到这里,关于 MLE 所有的知识点就讲完了,我们做个简单的梳理。
极大似然估计的目标,是通过观察样本估计某个参数的值,它估计的方法路径如下。
- 第一步,通过观察到的样本,建立代表这些样本发生可能性的似然函数。
- 第二步,利用求导法、梯度下降法等算法,求解似然函数的极大值。
- 第三步,用似然函数取得极大值的参数值,作为结果的估计值并输出。 在实际应用,样本很多的时候,通常认为样本之间是独立的,满足概率相乘的乘法法则;而面对连乘的复杂运算,通常采用对数似然函数的处理方式,化连乘为求和运算。
以上就是 MLE 基础原理的知识。
极大似然估计在工作场景中的应用
我们看一个利用极大似然估计解决实际工作问题的案例。
假设大迷糊是某个电商公司负责质量检测的工程师,这个公司的商品质量可以分为三档,分别是优质品、合格品和残次品。BI
的同事根据调研,发现商品的质量满足如下概率分布:
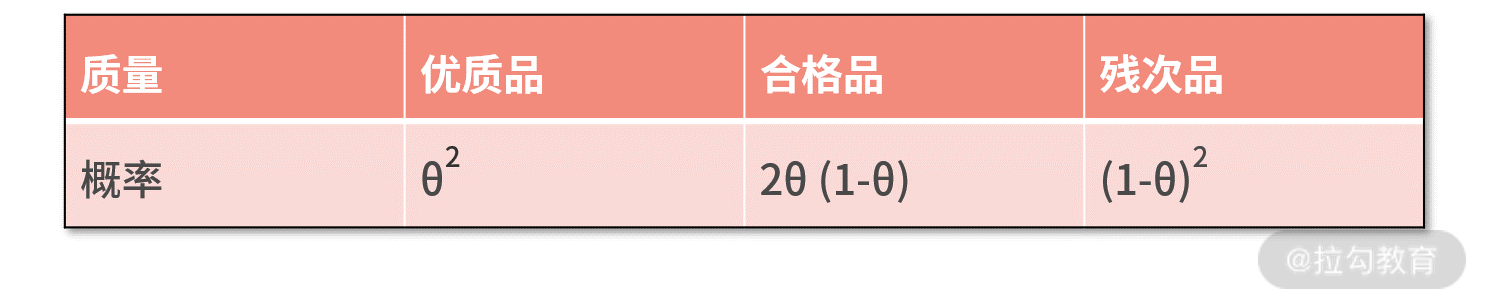
其中 θ 是个未知参数,大迷糊想用 MLE 的方法估计出 θ 的值。于是,大迷糊对商品进行了采样,得到的采样值分别为优质品、优质品和合格品。现在,让我们用
MLE 帮助大迷糊来估计未知数 θ 的值吧。
- 第一步 似然
我们发现,样本集合有 3 个样本,则 D = (d1,d2,d3) = (优质品,优质品,合格品)。待估计的未知数为θ,则似然函数为 P(D|θ) =
P(d1,d2,d3|θ) = P(d1|θ)·P(d2|θ)·P(d3|θ)。
代入 d1~d3 的值,以及对应的概率,则有 P(D|θ) = P(优质品|θ)·P(优质品|θ)·P(合格品|θ) = θ4 * 2θ(1-θ)。
那么,对数似然就是 ln P(D|θ) = ln (θ4 * 2θ(1-θ)) = ln 2 + 5 ln θ + ln (1-θ)。
- 第二步 极大
有了似然函数,我们就来尝试求解它的极大值吧。首先求对数似然函数关于 θ 的导数,则有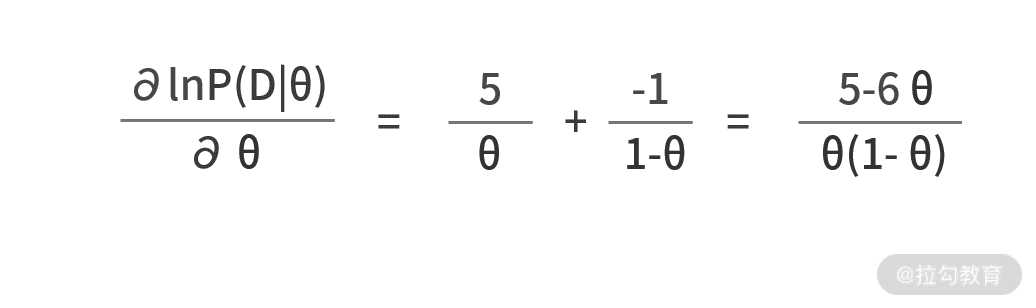
推导到这里,你会发现直接用求导法建立导函数为零的方程就能得到结果。这是因为,商品质量函数都是比较简单的多项式。如果里面包含了复杂的函数,例如指数函数、正弦函数等,就必须要借助梯度下降法来求解了。
为了再次说明梯度下降法的使用,我们这里尝试采用梯度下降法来求解,我们直接给出代码:
import math
def grad(x):
return (5 - 6 * x) / (x*(1-x))
def main():
a = 0.01
maxloop = 1000
theta = 0.1
for _ in range(maxloop):
g = grad(theta)
theta = theta + a*g
print theta
if __name__ == '__main__':
main()
我们对代码进行走读。
- 主函数中,设置学习率为 0.01,最大迭代轮数为 1000 次,θ 的初始值设置为 0.1。
- 接下来,第 10~12 行,是 1000 次的循环体。每次循环执行两个动作,分别是计算梯度,并把结果保存在 g 变量中;再用学习率和梯度的乘积,去更新 θ。
- 在计算梯度的函数 grad() 内部,直接返回一阶导数值。这是因为对于单变量而言,一阶导数的值就是其梯度的值。
我们执行这段代码,打印的结果如下图所示: 
如果我们用求导法,则有(5-6θ)/(θ*(1-θ)) = 0,解得 θ = 5/6 = 0.8333,这与我们用梯度下降法求得的结果一致。
- 第三步 估计
我们求解出的 θ* 值为 0.8333。它的含义是当 θ = θ* 时,大迷糊随机抽取 3
个样本恰好是优质品、优质品、合格品的概率最大。因此,我们有理由相信,θ* 是最有可能让这个观测结果出现的参数值。因此,0.8333 就是这里 θ
的估计结果。
小结
MLE 覆盖的知识点比较多。要想利用 MLE
去解决问题,你首先需要会计算概率,构建似然函数;接着,你还需要一些算法知识的储备,才能让你面对任何一个复杂函数,都能快速求解其最大值;最后,你还需要一个小技巧,那就是似然函数转化为对数似然函数后,最优估计值是不变的。
正是 MLE 的背后需要很多知识和能力,才让它成为数学学习过程中的一个难点。不过,庆幸的是,它的编程实现还是非常简单的。如果你掌握了梯度下降法的开发,那么
MLE 的开发也一定难不倒你。
最后,我们给一个练习题。假设在本例中,商品质量的分布如下:
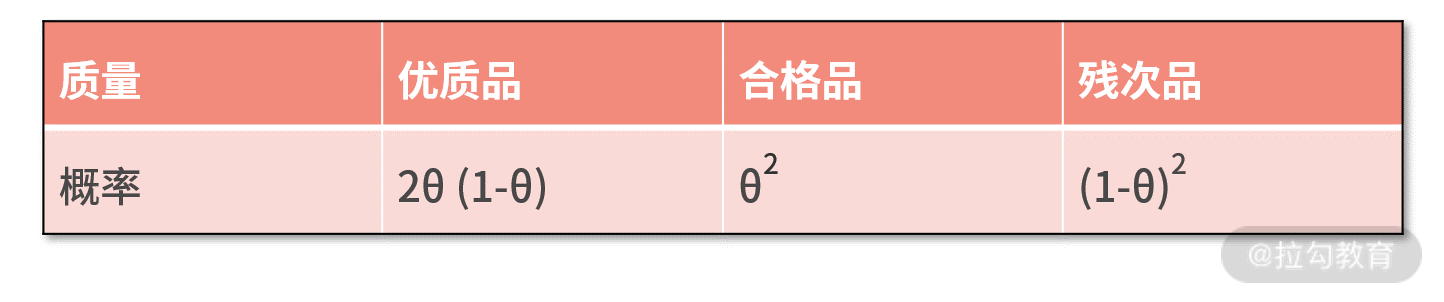
试着再来帮大迷糊来估计下 θ 的值吧。