21 神经网络与深度学习:计算机是如何理解图像、文本和语音的?
21 神经网络与深度学习:计算机是如何理解图像、文本和语音的?
在上一讲的最后,我们提到过“浅层模型”和“深层模型”。其实,人工智能的早期并没有“浅层模型”的概念,浅层模型是深度学习出现之后,与之对应而形成的概念。在浅层模型向深层模型转变的过程中,
神经网络算法无疑是个催化剂 ,并在此基础上诞生了深度学习。
这一讲,我们就来学习一下神经网络和深度学习。
神经网络的基本结构及其表达式
回想一下上一讲我们学的决策树,理论上来看,只要一直递归,一层又一层地寻找分裂变量,决策树做出预测的准确率是可以达到 100%
的。可见,这种层次化建立模型的思想,是不断提高模型效果的重要手段。
然而,对于决策树而言,AI 框架的第一个公式 y = f( _ w;x_
),只能被“画出”却很难用被写出。而这背后的原因,其实是决策树是一种类似于“if-else-”的条件分支结构,这本身就不是一种基于函数的数学表达形式。
那么我们不禁会想,有没有哪个模型既能保留层次化建模提高效果的优势,又能拥有基于函数的数学表达形式呢?
答案,就是神经网络。
神经网络是一种具有层次化结构的模型,它的设计来自生物学中对于人类大脑的研究。我们知道,神经元是人脑的基本结构,众多神经元组织在一起,就构成了人的大脑。
1.神经元,神经网络的基本单位
神经网络的结构与人类大脑结构非常相似,它的基本单位是函数化的神经元,再通过层次化地把这些神经元组织在一起,就构成了神经网络的表达式。
如下图,就是神经网络的神经元。
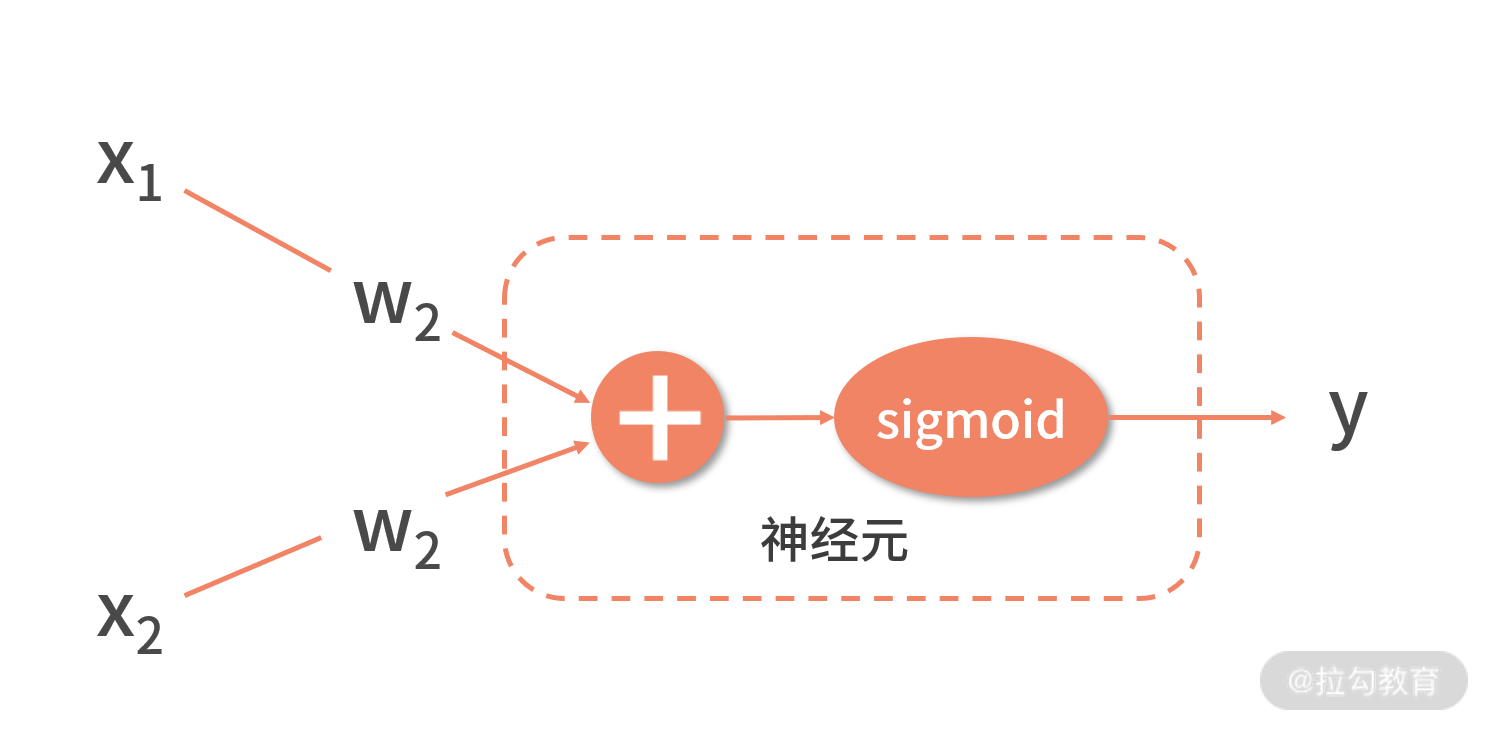
我们假设输入变量有两个。
实际中如果输入变量较多,只需要增加输入变量 xi 和权重系数 wi 的链接就可以了。
图中,x1 和 x2 是两个输入变量,它们分别与两个系数变量 w1 和 w2 相乘之后,指向了“+”号的模块。
得到了加权求和的结果之后,需要输入到一个 Sigmoid 函数中,最右的 y 就是这个神经元的输出,即
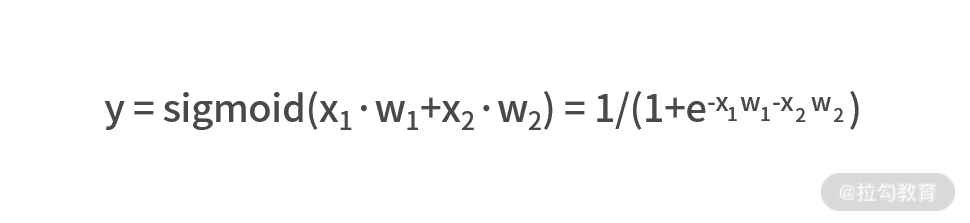
有了神经元的表达式之后,我们把图中虚线框的神经元用一个圆形的结点来进行封装,再把输出 y 写入这个结点中,这样就有了下面的表示形式。
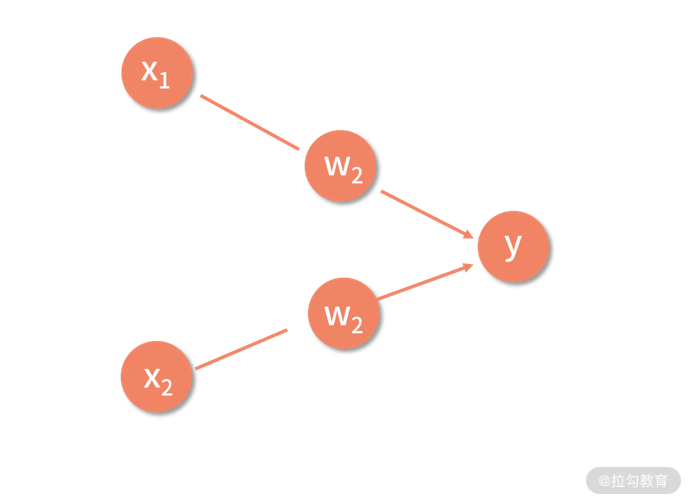
2.层次化将“神经元”构成神经网络
我们说过,层次化地把多个神经元组织在一起,才构成了神经网络。在这里, 层次化
的含义是,每一层有若干个神经元结点,层与层之间通过带权重的边互相连接。如下图,就是一个简单的神经网络。
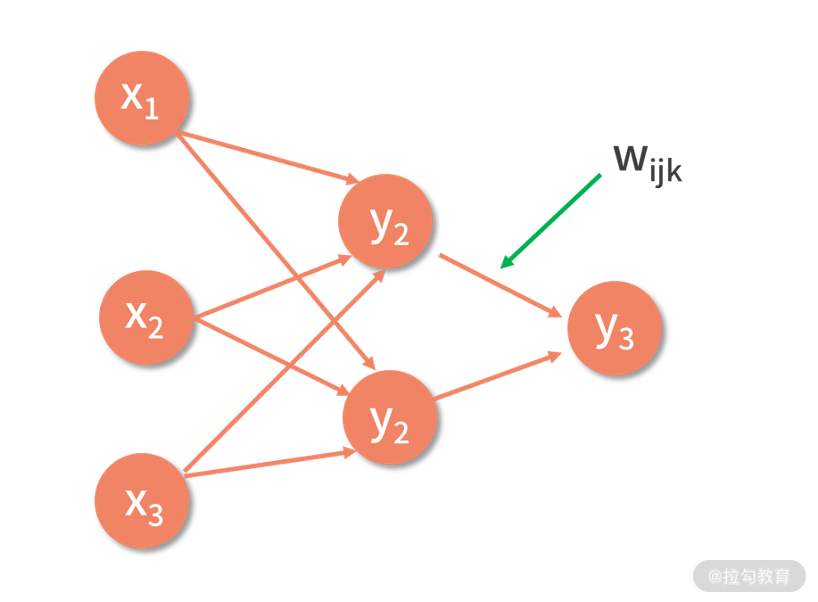
在这个神经网络中,输入变量有 3 个,分别是 x1、x2 和 x3。结点与结点之间,由带箭头的边连接,每条边都是一个权重系数
wijk。作用是将前面一个结点的输出,乘以权重系数后,输入给后面一个结点中。
这里 wijk 的含义,是第 i 层的第 j 个结点到第 i+1 层的第 k 个结点的权重。
网络中,除了最后一个结点以外,其余结点的输出都是临时结果;且每个临时结果,都将成为下一层神经元结点的输入。而最后一个结点的输出,也就是最终模型的输出 y。
对于神经网络而言,它既可以用图画的方式“画出”模型的结构,也可以通过函数化的形式写出输入和输出的关系,上图中的表达式如下。
y = y3 = sigmoid(y1w211+y2w221)
y1 = sigmoid(x1w111+x2w121+x3w131)
y2 = sigmoid(x1w112+x2w122+x3w132)
我们将 y1 和 y2 代入 y3,则有
y = sigmoid[sigmoid(x1w111+x2w121+x3w131) ·w211 +
sigmoid(x1w112+x2w122+x3w132)·w221]
虽然,神经网络模型可以用函数来写出输入输出关系的表达式,但由于网络结构本身的复杂性导致这个表达式并不好看。而且随着网络层数变多、每一层结点数变多,这个表达式会变得越来越复杂。
在实际应用中,根据需要神经网络可以有任意多个层次,每层里可以有任意多个神经元,这通常是由开发者自己根据问题的复杂程度而预先设置的。
神经网络的损失函数
有了神经网络的表达式之后,我们就继续用 AI
框架的第二个公式,去写出它的损失函数。神经网络的损失函数并没有什么特殊性,在绝大多数场景下,都会选择最小二乘的平方误差作为损失函数。
这一点,与线性回归是一致的。
最小二乘损失函数计算方式,是所有样本真实值 ŷ 与预测值 y 之间差值的平方和,则有:
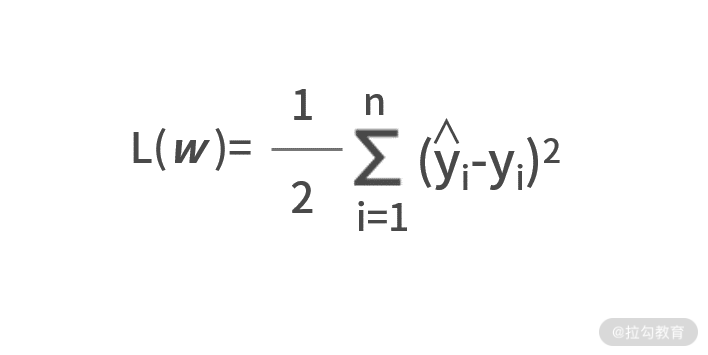
其中 n 代表的是所有的样本数。在这个损失函数中还有一个 1/2 的系数,增加一个系数会影响损失函数 L( _ w_ )
的值,但并不会影响最优系数的取值。
例如,y = 2x2+4和 y=x2+2 取得极值都是在 x=0 的点,之所以增加这个系数,是为了抵消后面平方项求导而产生的 2 倍的系数。
随机梯度下降法求解神经网络参数
最后,我们利用 AI 框架的第三个公式 _ w_ *= argmin L( _ w_ ),来求解神经网络。在神经网络中, _ w_
系数就是所有的 wijk。
我们把到现在为止的所有已知条件进行整理
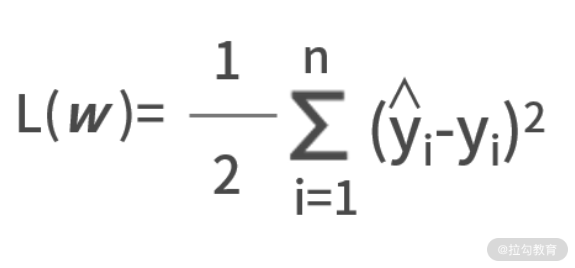
y = sigmoid[sigmoid(x1w111+x2w121+x3w131)·w211+sigmoid(x1w112+x2w122+x3w132)·
w221]
其中,对于某个给定的数据集而言,xi 和 ŷi 都是已知的。也就是说,我们要求解出让上面损失函数 L( _ w_ ) 取得极小值的 wijk
的值,我们可以考虑用先前学的随机梯度下降法来进行求解。
在使用随机梯度下降法的时候,只会随机选择一个样本(假设标记为 m)进行梯度下降的优化。因此,损失函数的大型求和符号就可以消灭掉了,即
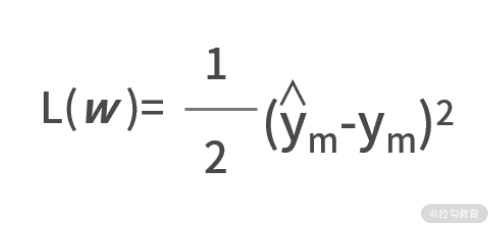
ym=sigmoid[sigmoid(xm1w111+xm2w121+xm3w131)·w211+sigmoid(xm1w112+xm2w122+xm3w132)·w221]
在这个例子中,我们有 8 个 wijk 变量,分别是
w111、w121、w131、w211、w112、w122、w132、w221,因此需要求分别计算损失函数关于这 8 个变量的导数。
既然表达式都有了,我们就利用大学数学求导的 链式法则 ,耐着性子来求解一下吧。
别忘了,y=sigmoid(x) 的一阶导数是 y·(1-y)。
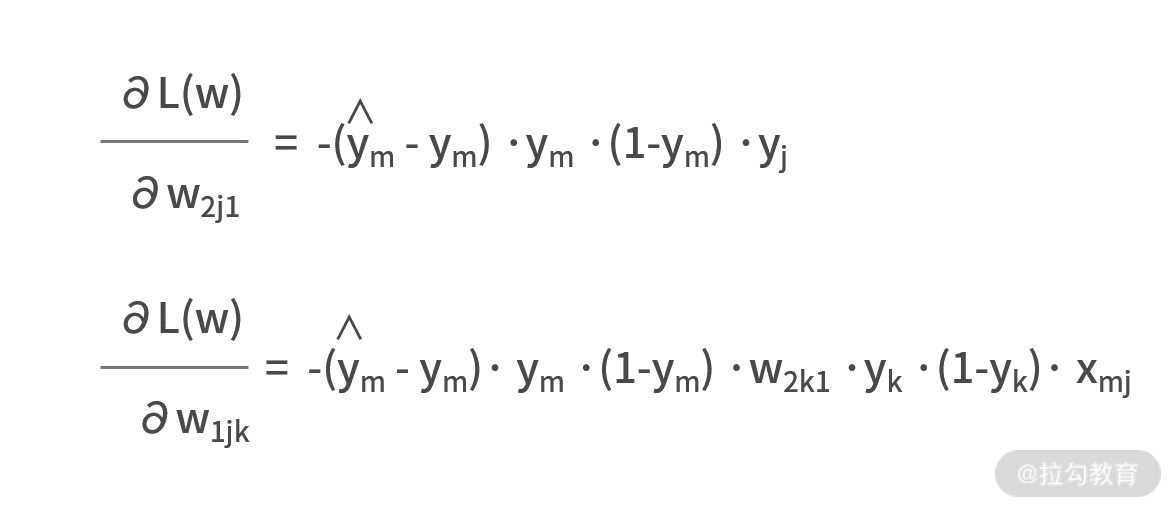
有了梯度之后,就可以设置学习率,再利用随机梯度下降法求解最优参数了。
神经网络建模案例
利用下面的数据集,建立一个神经网络。这个数据集中,每一行是一个样本,每一列一个变量,最后一列是真实值标签。
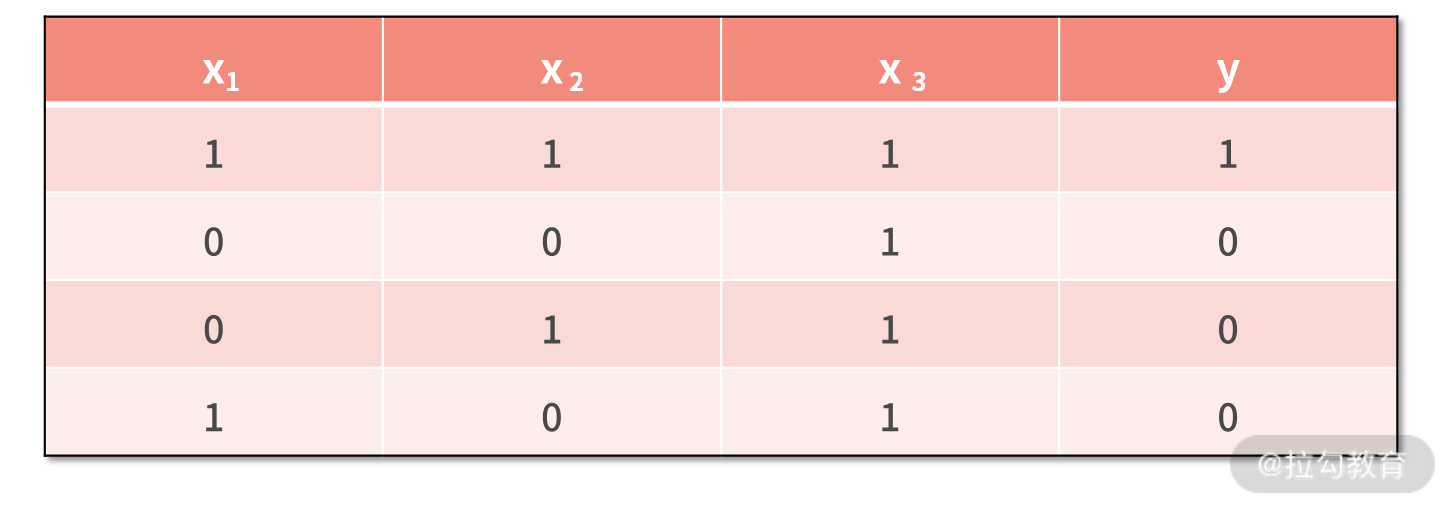
在利用神经网络建模时,需要预先设计网络结构。也就是说,你计划采用几层的网络,每一层准备设置多少个神经元结点。
我们看到,每个样本包含了 3 个输入变量。那么,我们可以直接采用上面推倒过的网络结构,即神经网络的结构如下所示。
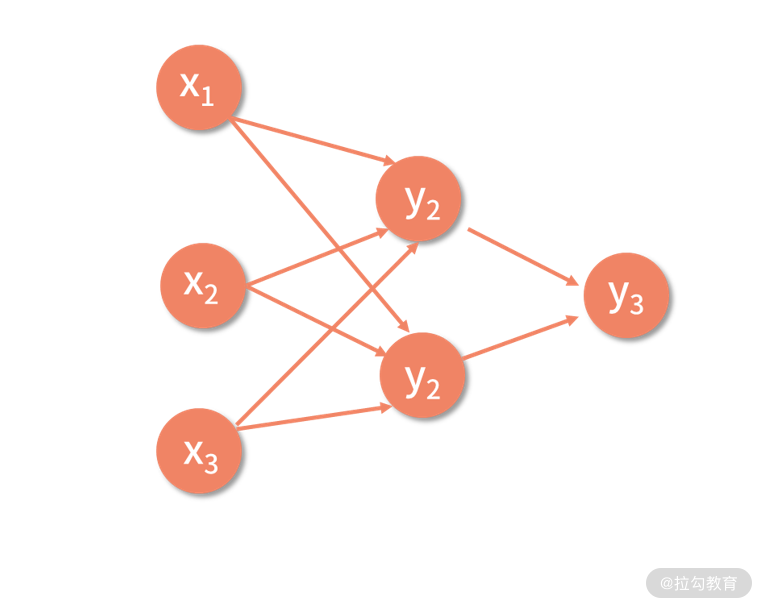
同时,我们也已经推导出了损失函数关于每个链接权重边的梯度,即
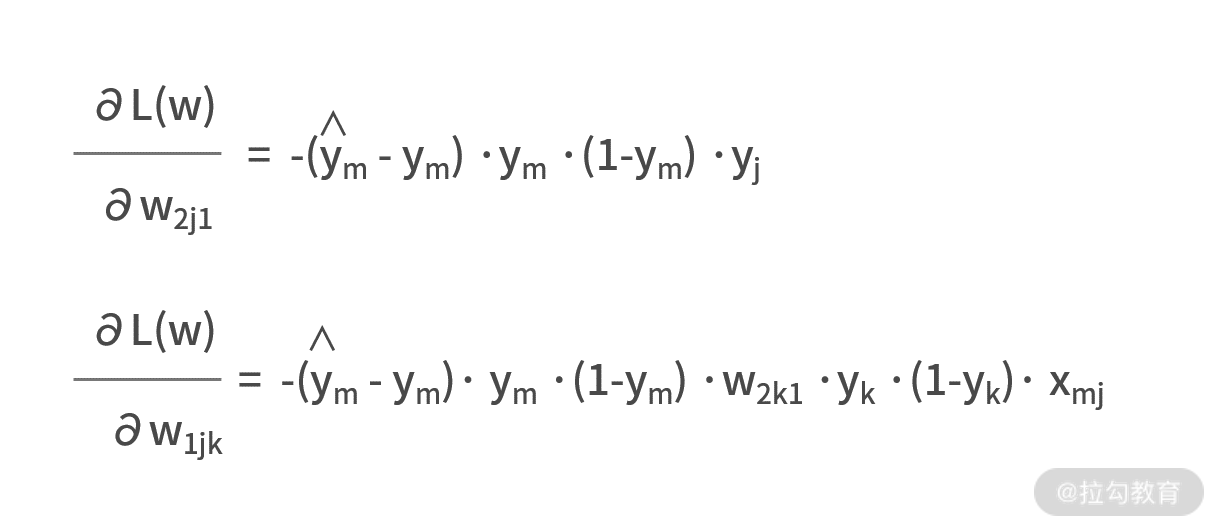
由于神经网络的代码量比较多,而且有非常多的开源工具可以使用。因此,我们这里给出伪代码,来展示其核心思想。
#获取数据集x和y
x,y = getData()
#随机初始化参数w
w = init()
#设置学习率
a = 1.0
#随机梯度下降法
for _ in range(1000):
index = random.randint()
y1,y2,y3 = getResult(x,w)
g = getGrad(x,y,w)
w = w - a*g
我们对代码进行解读:
- 第 2 行,读取数据集,并保存在变量 x 和 y 中,可以考虑用 Numpy 的 array 进行保存;
- 第 5 行,随机初始化参数向量 w,因为神经网络是多层、多结点的结构,所以可以考虑用个三维数组进行保存;
- 第 8 行,设置学习率,与以前的结论一样,如果迭代轮数够多,学习率可以考虑设置小一些;
- 第 11 行开始,进行随机梯度下降法的迭代。
- 第 12 行,调用随机函数,随机获取一个数据样本。
- 第 13 行,根据网络结构,计算 y1、y2、y3 每个结点的输出,其中还需要多次调用 Sigmoid 函数,可以考虑把 Sigmoid 的计算单独函数化;
- 第 14 行,根据梯度公式计算梯度值,并保存在 g 变量中,g 和 w 应该设置一样的数据类型;
- 第 15 行,利用梯度下降法进行参数更新。
在实际工作中,如果你需要建立神经网络的模型,除了上面自己开发代码的方式外,还可以考虑使用 Tensorflow 或者 Keras 等开源的人工神经网络库。
因为这只是实现的工具,原理上并没有什么差异,故而我们不再深入展开讨论。
神经网络和深度学习
深度学习通常指训练大型深度的神经网络的过程。
- 与传统的神经网络模型相比,深度学习模型在结构上与之非常相似;
- 不同的是,深度学习模型的“深度”更大,“深度”的体现就是神经网络层数多,神经网络每一层的结点数多。
下面,我们简单介绍两种深度神经网络——卷积神经网络和循环神经网络,以及它们分别在图像处理、文本处理和语音处理上的效果。
1.卷积神经网络(CNN)
与普通神经网络相比,卷积神经网络引入了“卷积”和“池化”两个操作,下面通过详细的例子,讲解卷积神经网络在图像处理的主要思路。
彩色图像由红、绿、蓝三原色组成,每种原色按照深浅可以表示为 0 到 255
间的一个数字。因此,对于图像中的每个像素(图像中不可分割的最小单位),都可以写出其相应的红、绿、蓝数值。
所以在计算机中,一幅彩色图像可由红、绿、蓝三个颜色的像素矩阵表示出来,下图给出了一幅 128×128 像素图像的矩阵表示:
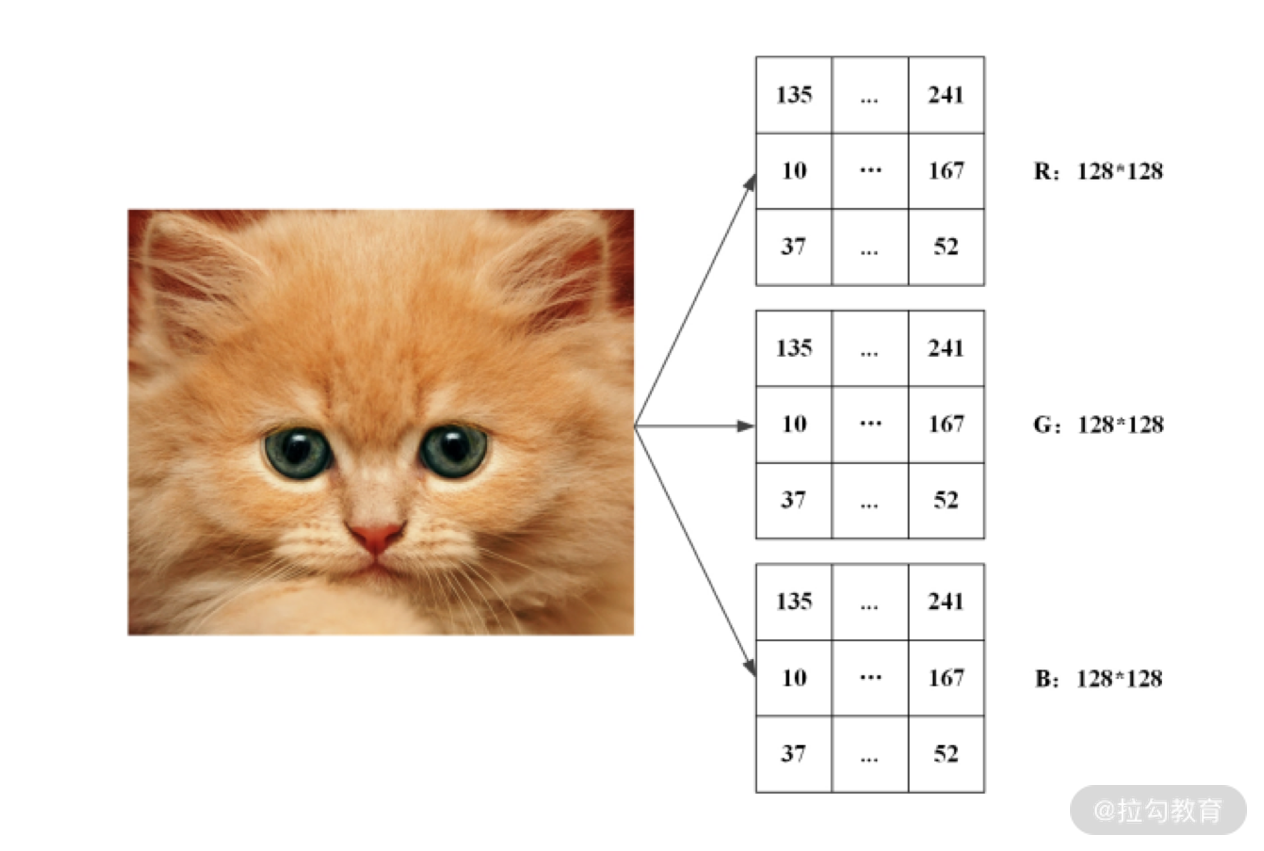
- “卷积”操作的思想 采用一个较小的卷积核,例如 3×3 的矩阵,来对图像特征进行局部的提取。这样做可以增加参数的共享,减少随着神经网络变深、结点数变多而带来的巨大计算量。
- “池化”操作的思想 采用一种过滤的方法,去除冗余信息并且加快计算。池化可以将一个 4×4 的图像切割成 4 个 2×2 的小矩阵,在每个小矩阵中取最大值,所得结果形成一个新矩阵。这种操作,可以减少神经网络结点的个数,加快计算速度。
在卷积神经网络中,通常某一个层都是在做卷积处理,某一层都是在做池化处理。一般,它们都是在层次之间交替进行的。经过多层卷积、池化操作后,所得特征图的分辨率远小于输入图像的分辨率,减少了计算量,加快了计算速度。
通过卷积和池化两项操作,卷积神经网络能在准确提取图像特征的同时,提升运算效率,因此在图像处理中取得了良好效果。
2.循环神经网络(RNN)
循环神经网络是一种善于处理序列信息的神经网络,在语音、文本处理方面有着非常大的优势。因为人类的自然语言属于一种时序信息,它有着明显的顺序关系,这就让以循环神经网络结构为基础的深度神经网络有其发挥空间。
除此之外,循环神经网络在引入 LSTM(Long Short-
TermMemory)结构后,在对有用时序信息的“记忆”和没用时序信息的“忘记”上有着强大的处理能力。
下图给出了一个 LSTM 的神经元结构。
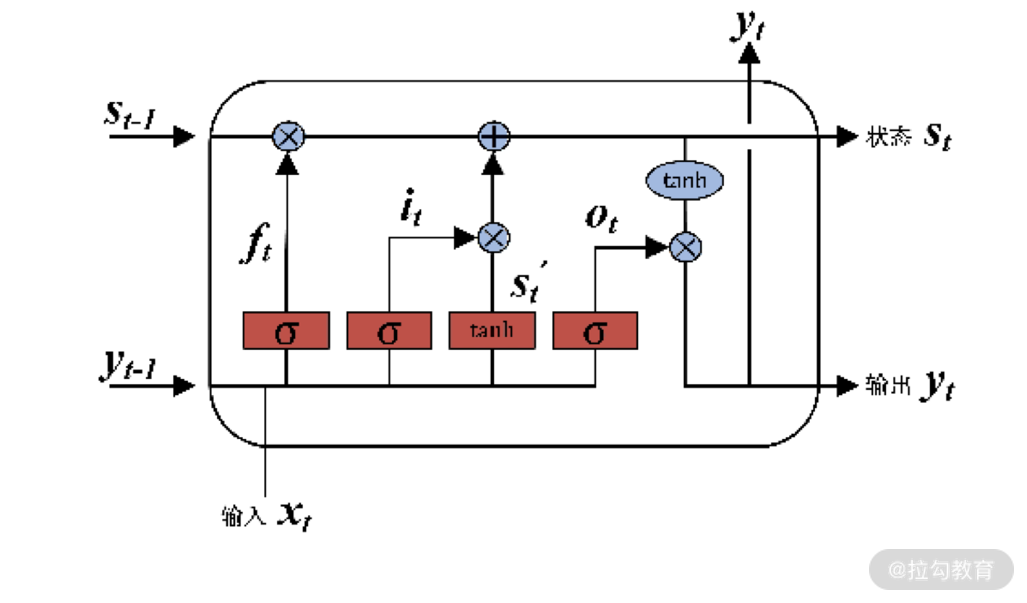
可以发现,LSTM
的网络结构和神经元结构已经非常复杂了,但它仍然保持着神经网络的那些特性。尤其是结构可被“画出”,输入、输出之间可以用函数表达。有了这些基本条件后,就仍然可以用损失函数和随机梯度下降法,来求解网络结构的参数。
小结
这一讲,我们学习了神经网络和深度学习。在当前的 AI
时代下,深度学习模型在效果方面打败了传统的浅层模型。而深度学习的基本原理都主要来自神经网络,神经网络结构可被“画出”,输入、输出之间可以用函数表达,这些特点都是支持它深度化的前提。
神经网络之所以能取得很好的效果,主要是因为网络结构的多样性。计算机在面对语音、图像、文本的不同问题时,主要是通过对网络结构进行优化迭代,设计出
CNN、RNN 的新型神经网络结构的。
此外,神经网络的损失函数和参数求解,仍然和其他浅层模型相似,并没有什么特别。
最后,我们给大家留一个练习题。假设有一个 4 层的神经网络,第一层是输入 xi,最后一层是输出 y。4 层的结点数分别是
3、2、2、1。试着去求解一下损失函数关于每个链接权重的梯度吧。